Solving partial WIF
What is a WIF?
R: Wallet Import FormatYou can found more details of a wif in Chapter 4. Keys, Addresses, Wallets
Solving WIF can be an impossible task or maybe an easy one all depend of what kind of data do you have.
There are some different scenarios
- Missing characters at the end.
- Missing characters in the middle
- Missing characters in the beginning.
Each case have different approach to solve it.
Also we need to considerate the next questions:
Where the WIF come from?
If the data of the WIF was taken from some YouTube video or some public picture on internet, please FORGET it, most of the WIF KEY from public internet sources are fake, just made to troll people.
How many missing characters are there?
If the amount of missing characters are near to the half of the WIF please also forget that WIF even if the WIF is real is near to impossible brute force the missing characters.
Missing characters at the end is the most easy case to solve because at the end of the WIF we have the checksum of the WIF so if only a few characters are missing you only need to check how much part of the KEY data you lose.
Lets to check this with an example with a uncompressed WIF:
WIF: 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
WIF decoded: 801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aeddc47e83ff
The firt byte is the Encode byte: 80
The next 32 bytes is the Privatekey: 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aedd
The last four bytes is the checksum: c47e83ff
For this example lets to say that you lost 10 characters at the end
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2Jpbnke**********
Lets to get the decode data two times, the first time filled with ONEs and the second time filled with Z
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2Jpbnke1111111111
801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc69f4e6e9680c6bc00
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2Jpbnkezzzzzzzzzz
801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a548f4bb48c25fff
if we remove the encoded byte and the last four bytes for the checksum we get the range where our key is:
from: 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc69f4e6e96
to: 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a548f4bb
In this example we lost near to 32 bits or 4 bytes of our KEY this can be recover easy using keyhunt or some other program that can scan ranges
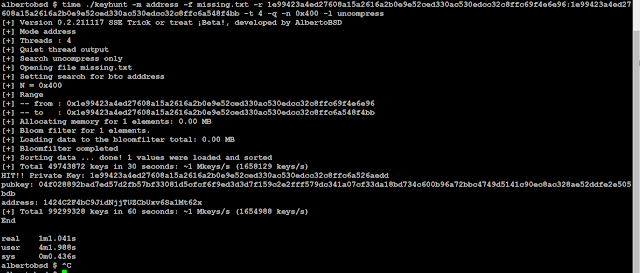
Save the address 1424C2F4bC9JidNjjTUZCbUxv6Sa1Mt62x in a file missing.txt and load it in keyhunt with the next parameters:
time ./keyhunt -m address -f missing.txt -r 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc69f4e6e96:1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a548f4bb -t 4 -q -n 0x400 -l uncompress
For address keyhunt is some slow :(, we can also search for the rmd160 hash "211b74ca4686f81efda5641767fc84ef16dafe0b" with 4 times more speed, save the hash in a new file and load it in keyhunt with the next parameters:
time ./keyhunt -m rmd160 -f missing_new.txt -r 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc69f4e6e96:1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a548f4bb -t 4 -q -n 0x400 -l uncompress
If you lost more than 50 bits and you don't have the publickey please forget the WIF, unless you have a powerful GPU to check your key range with another tool.
I said another tool because keyhunt is not made for GPU yet.
If you have the publickey you can recover up to to 70 or 75 bits in less than 10 hours, this also depend of you CPU speed and RAM memory.
Example with 16 missing characters at the end only if you have th PUBLICKEY
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2****************
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU21111111111111111
801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc2280d6175347c34ca88b0000
5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2zzzzzzzzzzzzzzzz
801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc577eb98d70ea2e7389cbffff
Following the same example as before you need to extract the KEY start and end range:
from: 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc2280d6175347c34c
to: 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc577eb98d70ea2e73
Save the publickey "04f028892bad7ed57d2fb57bf33081d5cfcf6f9ed3d3d7f159c2e2fff579dc341a07cf33da18bd734c600b96a72bbc4749d5141c90ec8ac328ae52ddfe2e505bdb" in a file and load it in keyhunt with the next parameters to use 23 GB of RAM:
time ./keyhunt -m bsgs -f publickey.txt -k 1536 -S -q -r 1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc2280d6175347c34c:1e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc577eb98d70ea2e73 -t 4
Also i make some video showing how to try to solve 67 bits in half hour.
Missing characters in the middle
Following our previous example the WIF 5J3mBbAH58CpQ3Y5RNJpUKPE62SQ5tfcvU2JpbnkeyhfsYB1Jcn
with hexadecimal value is 801e99423a4ed27608a15a2616a2b0e9e52ced330ac530edcc32c8ffc6a526aeddc47e83ff is going to have some missing characters in the middle:
5J3mBbAH58CpQ3Y5RN*******2SQ5tfcvU2JpbnkeyhfsYB1Jcn
if we fill the missin part with "1" an "z" we get the next two values:
5J3mBbAH58CpQ3Y5RN11111112SQ5tfcvU2JpbnkeyhfsYB1Jcn
801e99423a4ed27608a15a2615df3c6c0d8f98665c36bf9be3d15413537383fb0fa87e83ff
5J3mBbAH58CpQ3Y5RNzzzzzzz2SQ5tfcvU2JpbnkeyhfsYB1Jcn
801e99423a4ed27608a15a26185b73b7b0c3878ac5e6481d0f573a0622665b6241047e83ff
Removing the encode byte and checksum part seens that we have almost 21 Bytes (168 bits) missing, but this is not true.
1e99423a4ed27608a15a2615df3c6c0d8f98665c36bf9be3d15413537383fb0f
1e99423a4ed27608a15a26185b73b7b0c3878ac5e6481d0f573a0622665b6241
Every character in the WIF KEY has some position and one Related "Decimal value" Let's take the next example:
ALbertoBSD
This has the next hexadecimal value:
f66950c8f1a35e
But every character has his own value example:
A111111111 -> ed7ebf16344a00
1L11111111 -> 08a4fb2f65f300
11b1111111 -> 004446efcea500
111e111111 -> 000147f39f8740
1111r11111 -> 0000077cf943a0
11111t1111 -> 00000022667a30
111111o111 -> 0000000088f330
1111111B11 -> 00000000008368
11111111S1 -> 000000000005aa
111111111D -> 0000000000000c
If we add all those values we will get the f66950c8f1a35e value
Why I explain this to you?
Because there are two approach to Brute a incomplete wif:
- fill the missing parts with all the possible values from 1111111 to zzzzzzz
- find the correct stride and add to the star value and do this until the key is found
The first approach is the SLOWEST because the WIF key need to be decode in each posibility and each time that the key is decoded it requires almost 51 Additions operations to get the final value.
The second approach is FASTER because it only require only the Base Key in Decimal and ONLY ONE ADDITION in each possibility
How to calculate the number of possibilities?
Since we are talking of a base 58 string then each missing possition has 58 possibles values.
For this example we have 7 missing characters, then the number of possibilities is:
58^7 = 2207984167552
This is 2.2 Trillions of possibilities
How to calculate the correct stride for the current example?
Rudimentary example:
Take the right side of the string including it only the first missing character
12SQ5tfcvU2JpbnkeyhfsYB1Jcn
Remplaze the missing characeter with 2 and the remaining characters with 1
211111111111111111111111111
Use any tool or page like https://learnmeabitcoin.com/technical/base58 to decode the base58 string to hexadecimal
Value:
013cd125f2165f8510dba46008014a08a4000000
Math example:
Get the possition of the first missing character and subtract 1
X = (27 - 1) = 26
Calulate 58^X
58^26 = 7065254862732333761310239421614111190044114944
convert it to hexadecimal
013cd125f2165f8510dba46008014a08a4000000
From here you can use some tools by your own
bitcrack
WIFSolver (PawGo)
keyhunt (Only with publickey available and some publickey Transformations)
Here the link of some of the topics where I explain some related examples.
Missing characters at the END
This approach is very similar to the Middle approach but the main diferencte is that here you have to guess what kind of WIF it is, Compress or uncompress
Depening of the anwser you have to different WIF:
-Compress (52 Characters in the WIF, One Encode Byte at the beginning, One Encode post-byte and the end of the 32 bytes KEY, and the checksum)
-Uncompress (51 Characters in the WIF, One Encode Byte at the beginning and the checksum 4 bytes at the end of the decoded WIF)
Miscellaneous
There are several different subcases in each case
- There are publickey available?
- The stride overwrite the Checksum?
- The stride overwrite the Post-Encode Byte (Compress WIF)
- The stride overwrite the post-Encode Byte and Checksum
- Are the missing spliting in several parts of the WIF
Regards!


Comments
Post a Comment